Contenidos
Descubre qué es un ángulo obtuso, cómo medirlo y sus características clave. Aprende a identificar ángulos obtusos en figuras geométricas y encuentra ejemplos prácticos en la vida diaria.
Mejora tu comprensión con ejercicios resueltos y aplicaciones detalladas.
Tipos de ángulo obtuso
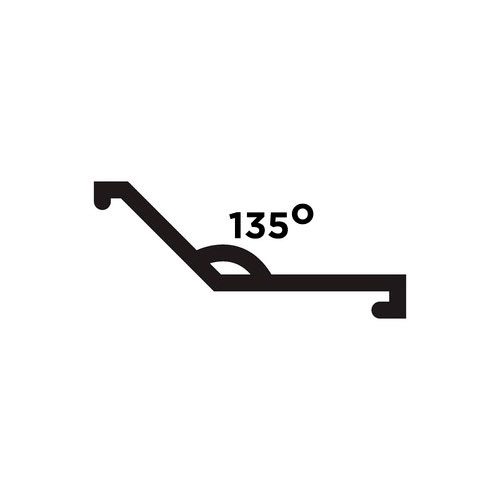
Un ángulo obtuso es un tipo de ángulo que siempre es mayor de 90° pero menor de 180°. En otras palabras, se encuentra entre 90° y 180°.
Ángulo obtuso de un triángulo
El ángulo obtuso de un triángulo es un triángulo, donde uno de sus ángulos de un triángulo es mayor que 90 grados. Un triángulo obtuso puede ser un triángulo isósceles o escaleno. Un triángulo equilátero no puede ser obtuso.
El ángulo opuesto al ángulo obtuso es el lado más largo del triángulo. De manera similar, un triángulo no puede tener un ángulo recto y un ángulo obtuso al mismo tiempo. Si uno de los ángulos de un triángulo es obtuso, los otros dos ángulos de un triángulo deben ser agudos.
Ángulo obtuso de un rombo
Un rombo es un cuadrilátero que tiene cuatro lados. Los ángulos opuestos de un rombo son congruentes entre sí. Un rombo tiene dos ángulos agudos opuestos congruentes y dos ángulos obtusos opuestos congruentes.
La suma de dos ángulos internos consecutivos es suplementaria. Significa que si se suman un ángulo agudo y el ángulo obtuso, su suma es 180 grados.
Ángulo obtuso de un paralelogramo
Los ángulos opuestos de un paralelogramo son paralelos entre sí. Un paralelogramo tiene lados paralelos. Significa que dos ángulos serán agudos y dos ángulos serán obtusos.
Dado que el paralelogramo se inclina, la medida del ángulo del ángulo obtuso será mayor y la medida del ángulo agudo será menor. Aquí, ∠A y ∠C son los ángulos agudos, mientras que ∠B y ∠D son los ángulos obtusos.
3 Ejercicios sobre ángulos obtusos con resolución:
Ejercicio 1:
En un triángulo, uno de sus ángulos mide 120° y los otros dos miden lo mismo. Si la suma de los ángulos interiores de un triángulo es 180°, ¿cuánto miden los otros dos ángulos?
Resolución:
- Sea x la medida de los dos ángulos iguales.
- La ecuación que representa la suma de los ángulos interiores del triángulo es: 120° + x + x = 180°.
- Combinando términos similares, obtenemos: 2x + 120° = 180°.
- Restando 120° de ambos lados de la ecuación, tenemos: 2x = 60°.
- Dividiendo ambos lados de la ecuación por 2, encontramos: x = 30°.
Por lo tanto, los dos ángulos iguales miden 30° cada uno.
Ejercicio 2:
Un edificio tiene forma de triángulo rectángulo, con un ángulo recto y dos ángulos obtusos. Si uno de los ángulos obtusos mide 135°, ¿cuánto mide el otro ángulo obtuso?
Resolución:
- En un triángulo rectángulo, la suma de los dos ángulos agudos es 90°.
- Como uno de los ángulos agudos es el ángulo recto (90°), el otro ángulo agudo debe medir 0°.
- La suma de los tres ángulos del triángulo es 180°.
- Por lo tanto, la ecuación que representa la suma de los ángulos del triángulo es: 90° + 135° + x = 180°, donde x es la medida del otro ángulo obtuso.
- Combinando términos similares, obtenemos: 225° + x = 180°.
- Restando 225° de ambos lados de la ecuación, tenemos: x = -45°.
Sin embargo, la medida de un ángulo no puede ser negativa. Por lo tanto, este problema no tiene solución.
Ejercicio 3:
Un arquitecto está diseñando una casa con forma de triángulo escaleno. Sabe que uno de los ángulos mide 80° y otro mide 50°. ¿Qué tipo de triángulo es la casa?
Resolución:
- La suma de los tres ángulos de un triángulo es 180°.
- La ecuación que representa la suma de los ángulos de la casa es: 80° + 50° + x = 180°, donde x es la medida del tercer ángulo.
- Combinando términos similares, obtenemos: 130° + x = 180°.
- Restando 130° de ambos lados de la ecuación, tenemos: x = 50°.
Como los tres ángulos miden 80°, 50° y 50°, la casa es un triángulo isósceles.
Explicación:
- Un triángulo isósceles es un triángulo que tiene dos lados y dos ángulos iguales.
- En este caso, la casa tiene dos ángulos que miden 50° cada uno.
- Por lo tanto, la casa es un triángulo isósceles.
Sobre el autor
-
Me interesa explorar cómo la tecnología, la economía y otros factores están afectando la forma en que las personas trabajan y buscan trabajo.
Me esfuerzo por proporcionar información útil y actualizada sobre las habilidades y los sectores que están creciendo, así como sobre los desafíos y las oportunidades que enfrentan los trabajadores en un mundo cada vez más cambiante.
Mi objetivo es ser una fuente confiable de información y orientación para aquellos interesados en el futuro del empleo.
Últimos Significados
Otros contenidos que pueden ser de tu interés a ¿Qué es un Ángulo Obtuso? Definición, Características los puedes visitar la categoría Matemáticas.
-
-
-
Kenai dice:
¡Interesante artículo! ¿Y qué tal si exploramos los ángulos obtusos en otras figuras geométricas como un pentágono o un hexágono? ¡Sería genial!
-
Narciso Fiol-Romero dice:
¡Buena idea! Los ángulos obtusos en figuras geométricas son fascinantes. ¿Qué otras curiosidades podríamos descubrir?
-
-
Marc Ferrero dice:
¡Interesante artículo! ¿Alguien más encuentra fascinante la geometría de los ángulos obtusos en diferentes figuras? 🤔📐
-
Hervé dice:
¡Interesante artículo! ¿Qué pasa si un ángulo obtuso es mayor a 120 grados? ¿Podría ser aún más obtuso? 🤔
-
Claro que sí, un ángulo obtuso puede ser mayor a 120 grados. ¡La geometría siempre sorprende! 📐✨
-
-
Auritz Comas dice:
¿Y si los ángulos obtusos fueran más interesantes de lo que pensamos? ¡Quizás tienen secretos geométricos por descubrir! 🤔📐
-
Montse Pozo dice:
¡Interesante artículo! ¿Se puede tener un ángulo obtuso en un círculo? Sería genial explorar más sobre eso. 🤔📐
-
Lucian Giron dice:
Claro que no, en un círculo todos los ángulos son de 90 grados. Investigación básica. 😉🔍
-
-
Andoni Castillo dice:
¡Interesante! ¿Y qué pasa con los ángulos obtusos en figuras más complejas, como los trapecios o los hexágonos? Sería genial explorar eso también.
-
Darrell dice:
¡Buena pregunta! Los ángulos obtusos en figuras complejas añaden un desafío interesante. ¡A investigar más!
-
Eliana D 
Deja una respuesta
Significados Relacionados